The Keccak hash design became the SHA-3 standard. KangarooTwelve is a hash based on the Keccak permutation, with a higher ingestion rate and fewer rounds than the SHA variants. It also allows for parallel processing. The code is here.
The permutation
The permutation operates on a state of 200 bytes, organized as
an array of 25 u64s. Each u64 is a "lane" of 64 bits.
The permutation consists of repetition of a "round";
24 rounds for SHA and 12 for KangarooTwelve (hence the name).
(the excellent diagrams are from the reference documentation)
a and produces next state efn round(a: &[u64], e: &mut [u64], c: &mut [u64]) {
let d = [c[4] ^ c[1].rotate_left(1),
c[0] ^ c[2].rotate_left(1),
c[1] ^ c[3].rotate_left(1),
c[2] ^ c[4].rotate_left(1),
c[3] ^ c[0].rotate_left(1)];
c[0] = 0; c[1] = 0; c[2] = 0; c[3] = 0; c[4] = 0;
macro_rules! row { ($i:literal, $d:literal) => {
let b0 = (a[PI[$i + 0]] ^ d[($d + 0) % 5]).rotate_left(RHO[PI[$i + 0]]);
let b1 = (a[PI[$i + 1]] ^ d[($d + 1) % 5]).rotate_left(RHO[PI[$i + 1]]);
let b2 = (a[PI[$i + 2]] ^ d[($d + 2) % 5]).rotate_left(RHO[PI[$i + 2]]);
let b3 = (a[PI[$i + 3]] ^ d[($d + 3) % 5]).rotate_left(RHO[PI[$i + 3]]);
let b4 = (a[PI[$i + 4]] ^ d[($d + 4) % 5]).rotate_left(RHO[PI[$i + 4]]);
let e0 = b0 ^ (!b1 & b2); e[$i + 0] = e0; c[0] ^= e0;
let e1 = b1 ^ (!b2 & b3); e[$i + 1] = e1; c[1] ^= e1;
let e2 = b2 ^ (!b3 & b4); e[$i + 2] = e2; c[2] ^= e2;
let e3 = b3 ^ (!b4 & b0); e[$i + 3] = e3; c[3] ^= e3;
let e4 = b4 ^ (!b0 & b1); e[$i + 4] = e4; c[4] ^= e4;
} }
row!( 0, 0);
row!( 5, 3);
row!(10, 1);
row!(15, 4);
row!(20, 2);
}This is the core of Keccak: u64 bitwise rotation, lane permutation,
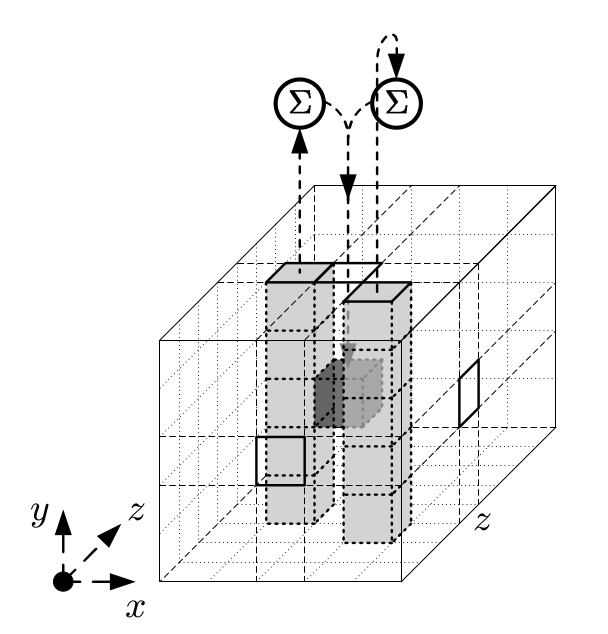
column sums, and intra-row bitwise combination. c is an array of
column sums, computed in the preceeding round. Those first five
lines computing d from the column sums corresponds
to the operation θ:
// c is an array of column sums
let d = [c[4] ^ c[1].rotate_left(1),
c[0] ^ c[2].rotate_left(1),
c[1] ^ c[3].rotate_left(1),
c[2] ^ c[4].rotate_left(1),
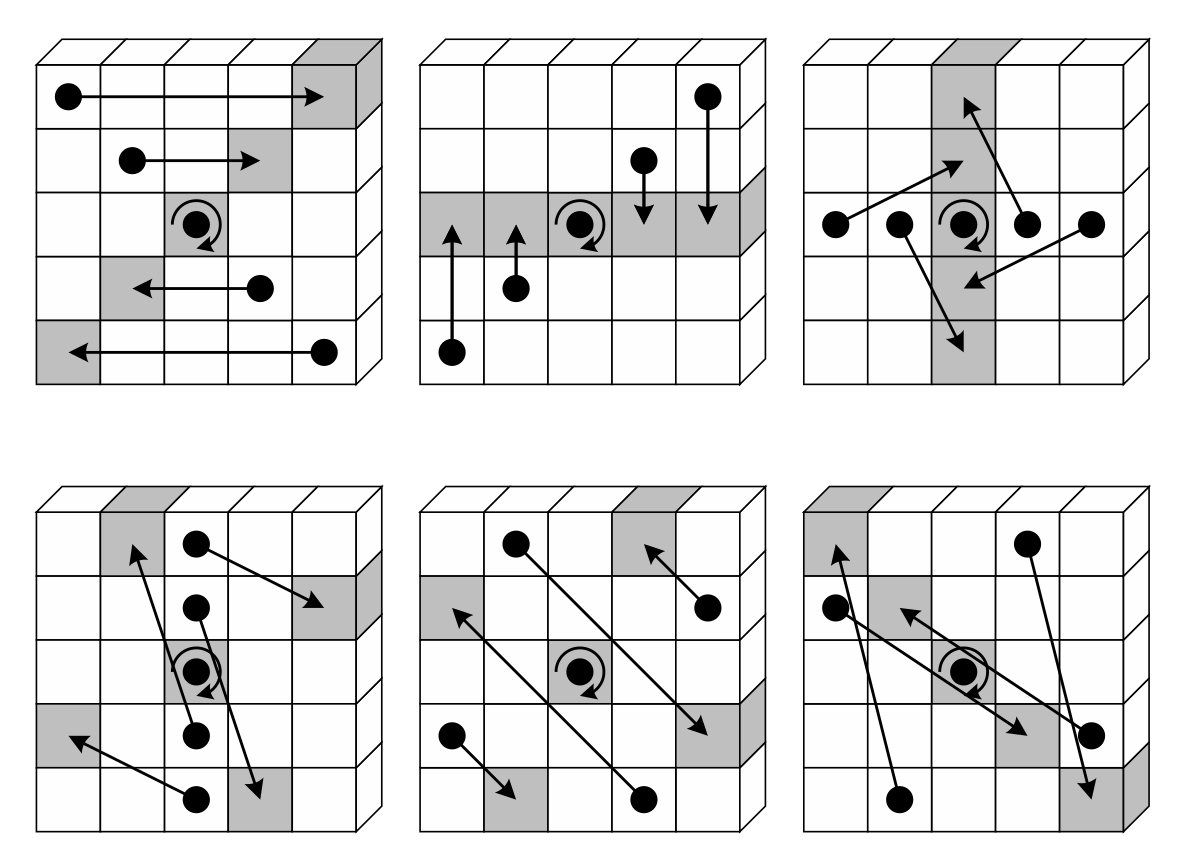
c[3] ^ c[0].rotate_left(1)];Loading from offsets defined by PI achieve the lane permutation
operation π:
a[PI[i]] // load at offset defined in PI
const PI: [usize; 25] = [
0, 1 + 5, 2 + 10, 3 + 15, 4 + 20,
3, 4 + 5, 0 + 10, 1 + 15, 2 + 20,
1, 2 + 5, 3 + 10, 4 + 15, 0 + 20,
4, 0 + 5, 1 + 10, 2 + 15, 3 + 20,
2, 3 + 5, 4 + 10, 0 + 15, 1 + 20,
];Rotating by offsets defined in RHO is the operation ρ:
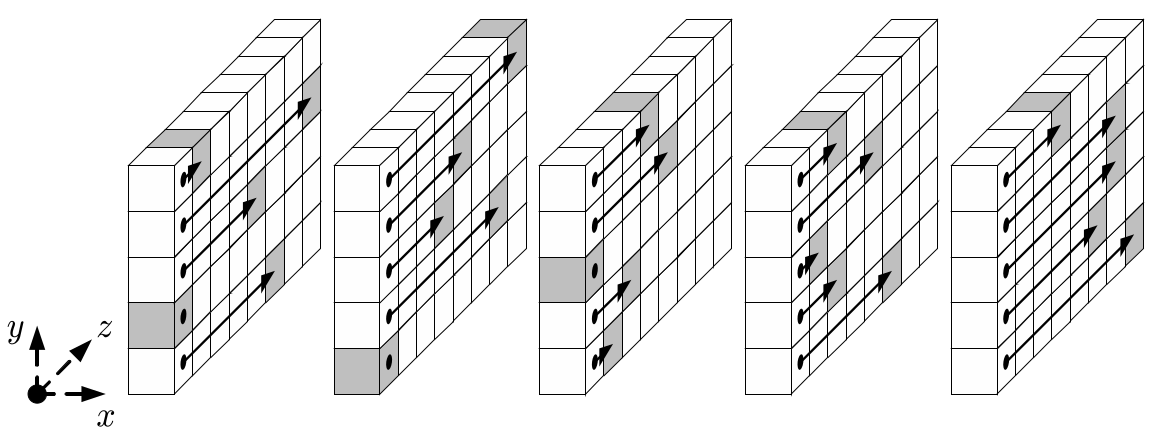
const RHO: [u32; 25] = [
0, 1, 62, 28, 27,
36, 44, 6, 55, 20,
3, 10, 43, 25, 39,
41, 45, 15, 21, 8,
18, 2, 61, 56, 14,
];And the operation χ applied within each row:
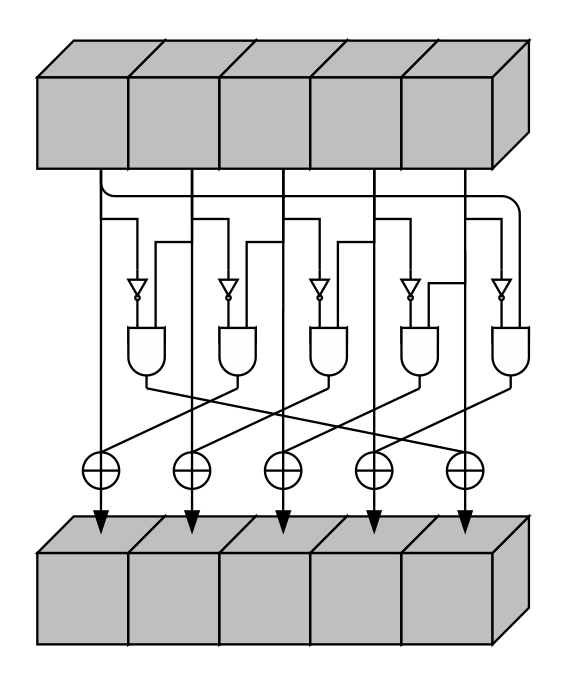
let e0 = b0 ^ (!b1 & b2);
let e1 = b1 ^ (!b2 & b3);
let e2 = b2 ^ (!b3 & b4);
let e3 = b3 ^ (!b4 & b0);
let e4 = b4 ^ (!b0 & b1);The sponge state machine
Instead of a one-shot, "gather all the bytes in memory"
interface, I wanted a state machine that you could
feed chunks of bytes into, piece by piece.
I defined struct Sponge to hold the necessary
state; the ingest method drives the state machine:
pub fn ingest(&mut self, bytes: &[u8]) {
let mut b = bytes;
loop {
let buf = self.state_as_buf();
if b.len() < buf.len() {
xor(&mut buf[..b.len()], b);
self.fill += b.len() as u8;
break;
}
xor(buf, &b[..buf.len()]);
b = &b[buf.len()..];
permute(&mut self.state, self.rounds);
self.fill = 0;
}
}It ingests bytes, filling the internal state, permuting when it’s full, and accounts for partial fills from previous chunks.
It is trivial to define a one-shot function on top of the state machine interface. I prefer this to having a one-shot only. This approach allows you to start hashing before the final byte has arrived.
pub fn sha3_256(m: &[u8]) -> [u8; 32] {
let mut sp = Sponge::new_256();
sp.ingest(m);
sp.finish(suffix::SHA);
sp.extract_32()
}The K12 state machine
After years of cryptanalysis on SHA-3, practical attacks could only make headway on reduced round variants with 5 or 6 rounds. There was a desire for a hash that trades some of the security buffer for better throughput.
KangarooTwelve (from the Keccak team) reduces the number of rounds to 12 down from 24, and ups the byte rate to 168 bytes at a time, up from 136 for SHA-256 and 72 for SHA-512. It also enables multiple 8k chunks of message to be hashed in parallel, combining each chunk result with a scheme called kangaroo hopping (hence the other part of the name).
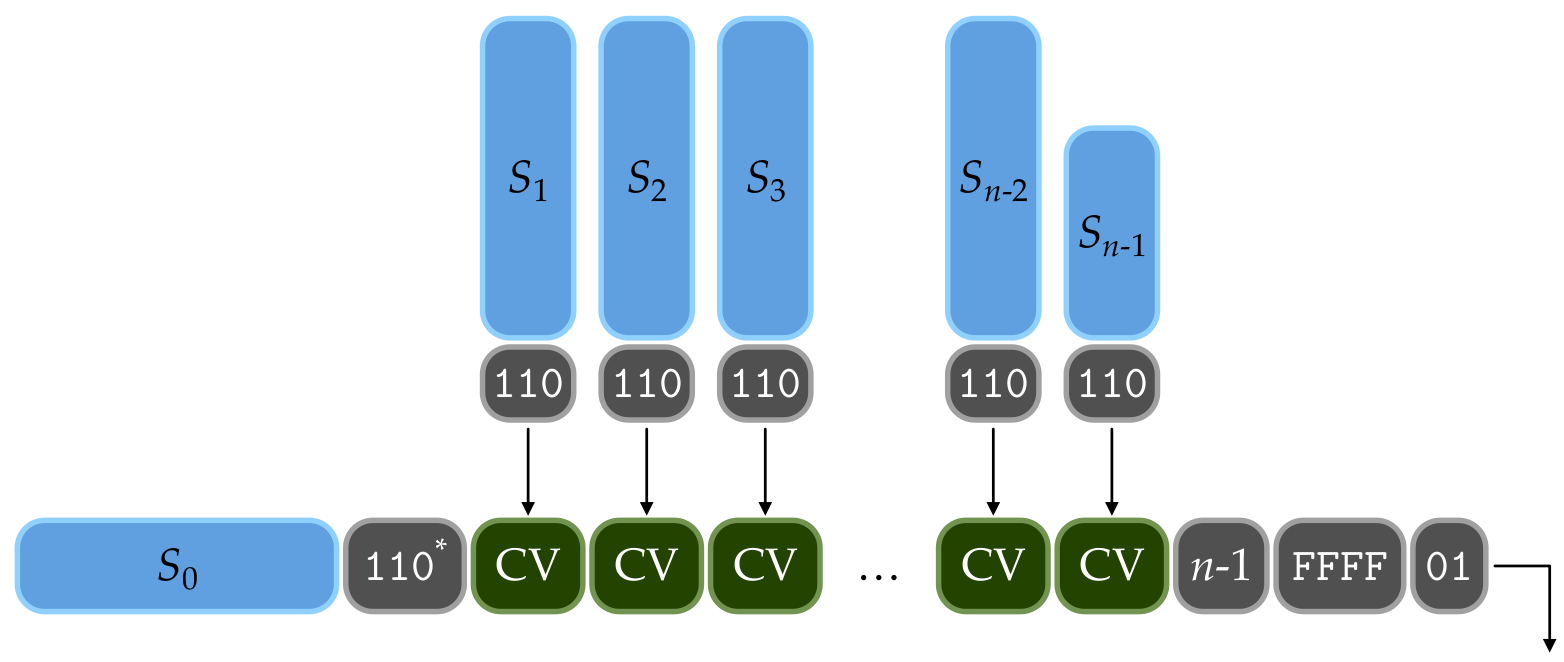
S is split in 8k chunksAgain, I wanted a state machine that could ingest the message piece by piece.
It builds on the first state machine, and it accounts
for a customization string, 8k boundaries, and the hopping scheme.
There is a familiar looking loop in the K12 state machine:
fn leaf_ingest(&mut self, bytes: &[u8]) {
let mut b = bytes;
loop {
let remaining = K12::SEG - (self.byte_count & K12::MASK);
if remaining > b.len() {
self.leaf.ingest(b);
self.byte_count += b.len();
break;
}
self.leaf.ingest(&b[..remaining]);
self.byte_count += remaining;
assert_eq!(self.byte_count & K12::MASK, 0);
self.leaf.finish(suffix::K12_LEAF);
self.trunk.ingest(&self.leaf.extract_32());
self.leaf.reset();
b = &b[remaining..];
}
}This code iteratively ingests 8k chunks and, when a leaf is full,
folds the result into the trunk sponge. Again, a one-shot
function can be trivially defined in terms of the state machine:
pub fn k12(msg: &[u8], custom: &[u8], digest_len: u32) -> Vec<u8> {
let mut k = K12::new();
k.ingest(msg);
k.finish(custom);
k.squeeze_vec(digest_len)
}In the Keccak repository there is a KangarooTwelve implementation in Rust that is a pretty direct port from the Python reference implementation. The author asks a question in a comment:
...
if blockSize == rateInBytes {
// TODO: condition is nearly always false; tests pass without this.
// Why is it here?
KeccakP1600(&mut state);
blockSize = 0;
}The answer is that the while loop preceding this code does
not account for exactly filling the sponge (message lengths
that are a multiple of 168 bytes). So this if triggers a
final permutation when exactly full. The next question
is more interesting:
...
state[blockSize] ^= delimitedSuffix;
if ((delimitedSuffix & 0x80) != 0) && (blockSize == (rateInBytes-1)) {
// TODO: condition is almost always false — in fact tests pass without
// this block! So why is it here?
KeccakP1600(&mut state);
}
state[rateInBytes-1] ^= 0x80;This logic comes from the reference implementation, which supports
messages of arbitrary bit length. For SHA-3, it is well defined to hash
a 7-bit message, for instance. The padding scheme places a single 1
bit after the last message bit, and another 1 bit at the very end of the buffer.
delimitedSuffix is a single byte that holds the final (0-7) bits of
a message, and the delimiting 1 bit.
This if detects the situation where the message has 7 bits at the end,
and the sponge has 8 bits until it’s full. For example, SHA-256 operates
on 136 bytes at a time, so a message of 135 bytes and 7 bits would
trigger this condition. Since it has 7 bits, the top bit is set
in delimitedSuffix, the first 1 bit of padding. Where will the
second 1 bit go? The sponge is now exactly full (there’s not room for
even one more bit), so we have to
perform a permutation before adding in the final 1 bit:
state[rateInBytes-1] ^= 0x80;The author notes that the tests pass without this if. In fact,
KangarooTwelve is only defined on whole-byte messages, and the delimited suffixes
never contain 7 bits. So this if will never be triggered, and is vestigial.
Looking forward
When I implemented the Keccak permutation a few years ago, I looked at all kinds of implementations and read anything I could get my hands on about different strategies. I took the same approach with the KangarooTwelve this summer. I believe it’s important to understand what other people have done. And I think it paid off.
The next steps are to test messages close to 8k boundaries, and messages passed in arbitrary pieces. Some randomized testing against a reference implementation would do quite well for this.
The round function performs dozens of length checks, every time the
slices a, e, and c are indexed. Better to do a few length asserts up front
and use slice.get_unchecked() in the body: fewer branches
in the emitted code. Writing unchecked all over would make a mess,
so I’ll probably use a local function, or another local macro.
This may not have a huge effect, but it’s low hanging fruit.
KangarooTwelve allows hashing the 8k leaf segments in parallel. This can be done with SIMD; you could permute four leaf segments simultaneouly for example. And you can have separate threads work on different leaves, joining their results at the end. It would take some experimentation to find what size of message would benefit from this parallelism, but for large messages parellelism could be a big win.